非线性仿真的基石：一条应力应变曲线的自我修养

在有限元仿真中，我们常常面临一个核心矛盾：为了精确预测产品的力学行为，必须使用非线性分析；而非线性分析的准确性，几乎完全依赖于输入的材料本构模型。其中，真实且准确的应力应变曲线是定义材料非线性行为的关键。那么，这条至关重要的曲线从何而来？

本文将深入探讨非线性材料应力应变曲线的获取方法、理论公式及其在仿真中的应用。

一、为何需要非线性曲线？—— 从理想走向真实

在简单的线性弹性分析中，我们只需输入杨氏模量E和泊松比v，材料行为完全由广义胡克定律描述：

σ=E：ε

其中C是四阶弹性张量。这只适用于材料在小变形下的初始弹性阶段。

然而，当应力超过材料的比例极限后，材料进入弹塑性阶段，其本质特征是不可恢复的塑性变形和应力-应变关系的非线性。此时，我们需要一条完整的应力应变曲线来定义：

1. 屈服点：塑性变形开始的应力σy

2. 硬化行为：屈服后，应力随塑性应变增加而变化的规律（硬化或软化）。

因此，获取非线性应力应变曲线的过程，本质上就是通过物理实验来揭示和量化材料超越弹性极限后的真实力学响应。

二、实验获取：从原始数据到工程曲线

最基础也是最可靠的方法是通过单轴拉伸试验。试验机对标准试样施加轴向拉力，同时记录载荷F和位移Δd，从而得到原始的载荷-位移曲线。

1. 工程应力与工程应变

最初得到的是最容易计算的工程值：

其中A0和L0是试样的初始横截面积和初始标距。

局限性：工程曲线在试样出现“颈缩”（Necking）现象后便失去意义，因为它使用的是不变的初始面积A0。实际上，在颈缩后，试样局部面积迅速减小，其承受的真实应力远高于工程应力。

2. 真实应力与真实应变

为了描述材料在均匀塑性变形直至颈缩前的真实行为，我们需要将其转换为真实值。假设变形过程中体积不变（A0L0=AL），则：

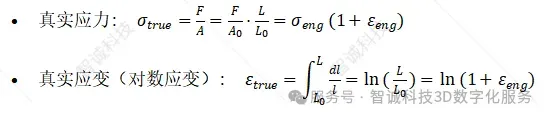
理论意义：真实应变具有真实性，更适合描述大变形过程。在有限元仿真中，尤其是使用Lagrangian方法时，输入基于真实应力-真实应变的曲线是更精确的选择。

三、在仿真中的建模：从数据点到本构模型

在FEA软件中，我们无法直接输入一条连续的曲线，而是需要将实验数据点拟合成一个硬化模型。常见的模型有：

双线性模型：用两条直线近似，一条是弹性段（斜率为 E），另一条是塑性段（斜率为Et ，切线模量）。

多线性模型：使用多个数据点连成的折线来更精确地拟合实验曲线。

幂律硬化模型（Swift/Voce模型）：使用一个数学公式来描述整个塑性段，这是最常用且高效的方法。

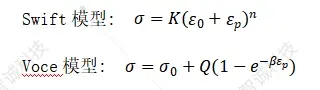
其中，σ是真实应力，εp是真实塑性应变，这是仿真输入的关键。它由真实总应变减去弹性应变得到：

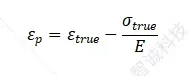
K，n，εp或σ0，Q, β 是需要通过曲线拟合算法从实验数据中确定的材料参数。

总结

获取一条准确的非线性材料应力应变曲线，是一个融合了实验力学、材料科学和数值分析的严谨过程。从简单的工程值，再到拟合成本构模型参数，每一步都至关重要。这条曲线不仅是连接虚拟世界与物理世界的桥梁，更是确保我们的非线性仿真结果可信、可靠，最终能够指导创新设计和工程决策的基石。