仿真视界 | 复杂应力怎么算？让Von Mises应力来帮忙

在材料力学中，对于材料的失效一共有四大强度理论。其中第四强度理论又被称为最大畸变能理论，且广泛用于解决实际的工程问题。这是因为在实际的工况中，材料各处受到的力极为复杂，并不是简单的正应力或者剪切应力。

以一个单元体为例，在一面上施加拉伸载荷，其受到的是一个正应力，记为σ1。从宏观上看，单元体沿载荷方向伸长，但因为泊松效应在另外两个方向上缩短。根据广义胡克定律：

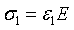
和泊松比：

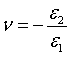
扩展一下可得：

（1.1）

材料强度不足引起的失效现象主要分为屈服和断裂两种类型，相应的强度理论也分成两类：一类是解释断裂失效的，其中有最大拉应力理论和最大伸长线应变理论。另一种是解释屈服失效的，其中有最大切应变理论和最大畸变能理论。

对于最大畸变能理论而言，一般认为是畸变能密度达到某一极限值，材料就发生失效。那么该如何判断其畸变能密度呢？

我们假设对一弹性体做功，载荷大小为P，变形量为x。则有U=Px/2,其中U为做功的总能量。我们现在对等式两边同时除以体积，可以得到单位应变能，即：

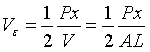
其中体积可以用面积A乘以长度L替代，再发现：

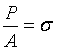
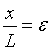
故我们可以将单位体积的应变能记为：

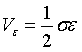
现在我们将设对于这个单元体施加多项载荷，对于弹性变形我们可以通过叠加原理得到其应变能密度为：

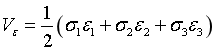
(1.2)

根据式（1.1）可得：

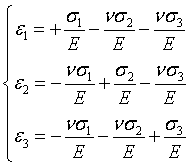
(1.3)

将式（1.3）带入式（1.2）可得复杂载荷下的应变能密度为：

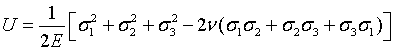
(1.4)

通过引入平均正应力，可以将总应变能分解为体积和形状改变能两部分，即总应变能 = 体积变形能 + 形状改变能：

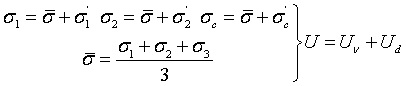
(1.5)

由于Uv恒定，可以视为静水压导致体积变化，形状改变能才是导致材料失效的主要原因。将式（1.5）带入式（1.4）可得：

(1.6)

根据式（1.6），即认为无论什么应力状态，只要畸变能密度Ud

达到与材料性质有关的某一极限值，材料就发生屈服。为简便计算，我们假设对一材料仅施加一正轴载荷，对应的畸变能密度为：

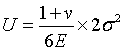
此时，材料的畸变能失效准则为：

(1.7)

此时，材料的屈服准则可简化为“Von Mises应力等于屈服强度”（σᵥ= σₛ），这一形式简洁且便于工程计算，因此成为复杂应力状态下判断材料屈服的核心指标。