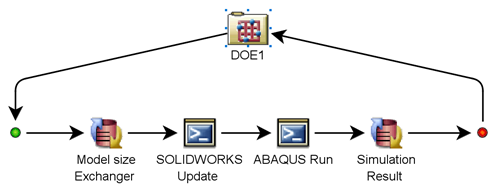
仿真视界 | JC本构模型参数拟合秘笈：如何“分而治之”搞定材料仿真难题？

J-C本构在冲击动力学中是应用最为广泛的本构模型，其模型方程如下：

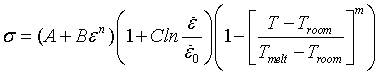
可以看到J-C本构的主体由三部分构成，分别表征了材料的应变硬化、应变速率强化以及热软化。模型全方位考虑了流变应力与应变、应变速率以及温度之间的关系，能够满足各种条件下的仿真材料需求。需要指出的是J-C本构，采用简单的乘积形式将三项联立，说明模型只是单独考虑了应变、应变速率和温度的影响，而并未考虑各因素之间的耦合影响，所以在一些特殊情况下模型的精度可能会存在一些问题，因此在J-C本构的基础上也有很多研究，对其进行了修正。J-C的简单乘积形式带来的好处是，在参数的拟合上可以分开拟合，十分简洁。

模型中A，B，n，C，m为五大材料物理特性常数，下一部分将简要讲述拟合获取方式。

在室温及参考应变速率条件下开展试验时，本构模型中的应变速率项与温度项均退化为常数1。参数A表示该实验条件下的初始屈服应力。对实验数据取对数后，可得到线性关系，通过拟合直线的斜率和截距，即可求解出参数n和B。至此，模型第一部分的参数A、B和n全部确定。

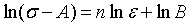
在室温条件下进行不同应变速率下的试验，选取相同应变对应的应力值进行拟合。由于温度项在室温下仍为1，且在同一应变下应变硬化项也为固定值，该值可通过前一步拟合结果计算得出。此时，本构模型可简化为一次方程形式。通过对实验数据进行线性拟合，即可得到应变速率常数C。

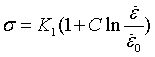
温度常数m的拟合思路与应变速率常数C相似。首先，在固定应变速率下，进行一组不同温度的试验，并选取相同应变下的应力数据。此时，结合前两步已求得的参数，模型可简化为仅含温度项的函数关系。

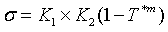
对该关系式两边取对数，可将问题转化为线性拟合，拟合所得直线的斜率即为热软化指数m的值。至此，Johnson-Cook本构模型的五个核心参数已全部确定。