SOLIDWORKS函数解析大全

利用SOLIDWORKS方程式，我们可以实现零部件直接的参数设计，实现用少量的数据变化驱动整个模型，但是在使用中我们的算式都是由加减乘除组成，导致需要输入的数据过多。下面给大家讲解一下SOLIDWORKS方程式的函数是什么意义，如何去写方程式？

首先给大家介绍一下，SOLIDWORKS方程式里面的函数是在哪里输入的，在<工具>菜单栏上选取<方程式>,输入全局变量名称，点击<数值/方程式>选取<函数>，如图所示

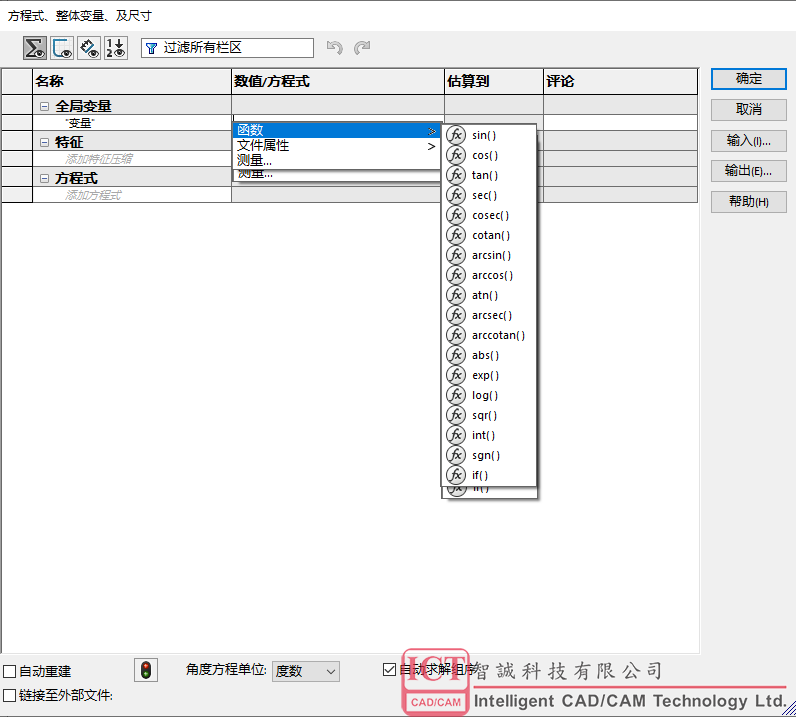
里面涉及到的函数1.sin() 2.cos() 3.tan() 4.sec() 5.cosec() 6.cotan() 7.arcsin() 8.arccos() 9.atn() 10.arcesect() 11.arccotan() 12.abs()  13.exp() 14.log() 15.sqr() 16.int() 17.sgn()  18.if()  共18种分为七大类型


一、三角函数函数
sin() 、cos() 、tan() 、sec() 、cosec() 、cotan() 、arcsin() 、arccos() 、atn() 、arcesect() 、arccotan()

1. 三角函数 sin()、cos()、tang()、cotan()、sec()、cosec()

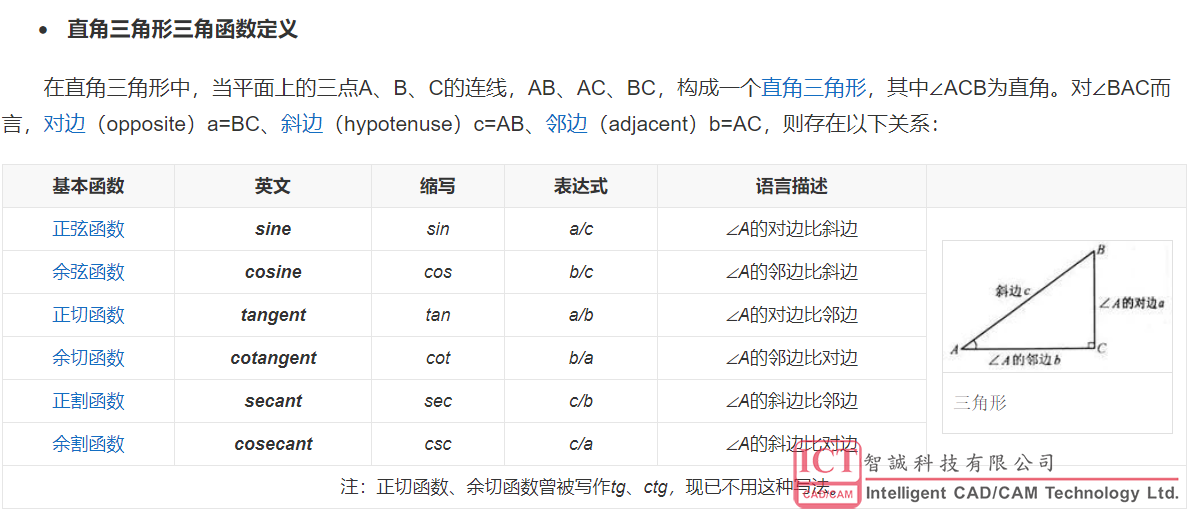
用法：括号内填（a）    a=夹角角度

1. 反三角函数 arcsin()、arccos()、atn()、arccotan()、arcsec()、arccos()
2. arcsin()：正弦函数y=sin x在[-π/2，π/2]上的反函数，叫做反正弦函数。记作arcsin(a)，表示一个正弦值为a的角，该角的范围在[-π/2，π/2]区间内。定义域[-1，1] ，值域[-π/2，π/2]。 
3. arccos()：余弦函数y=cos x在[0，π]上的反函数，叫做反余弦函数。记作arccos(a)，表示一个余弦值为a的角，该角的范围在[0，π]区间内。定义域[-1，1] ， 值域[0，π]。
4. atn()：正切函数y=tan x在（-π/2，π/2）上的反函数，叫做反正切函数。记作arctan(a)，表示一个正切值为a的角，该角的范围在（-π/2，π/2）区间内。定义域R，值域（-π/2，π/2）。
5. arccotan()：余切函数y=cot x在（0，π）上的反函数，叫做反余切函数。记作arccot(a)，表示一个余切值为a的角，该角的范围在（0，π）区间内。定义域R，值域（0，π）。
6. arcsec()：正割函数y=sec x在[0，π/2）U（π/2，π]上的反函数，叫做反正割函数。记作arcsec(a），表示一个正割值为a的角，该角的范围在[0，π/2）U（π/2，π]区间内。定义域（-∞，-1]U[1，+∞），值域[0，π/2）U（π/2，π]。
7. arccos():余割函数y=csc x在[-π/2，0）U（0，π/2]上的反函数，叫做反余割函数。记作arccsc(a)，表示一个余割值为a的角，该角的范围在[-π/2，0）U（0，π/2]区间内。定义域（-∞，-1]U[1，+∞），值域[-π/2，0）U（0，π/2]。

用法：括号内填（a）    a=夹角角度

• 取整函数 int()
  用法“N”=int("RD1@注解")         含义:对"RD1@注解"取整
• 平方根 sqr()

用法：“N"=spr("RD1@注解")        含义:N等于"RD1@注解"的开平方方

• 对数函数log()
  用法：“N"=log("RD1@注解")     含义： ("RD1@注解")等于角度
• 指数函数 exp()

用法:“N"=exp(2)即 n=e^2 (e≈2.71828)

• 绝对值函数 abs()
  用法：“N”=abs("RD1@注解")         含义:对"RD1@注解"取绝对值
• 条件函数  if()
• 用法：例:"N"=if("RD1@注解"<=4700,4,iif("RD1@注解"<=5600,5,5))
  含义:当"RD1@注解"<=4700 时，N=4，当 4700<"RD1@注解"<=5600 时，N=5，当"RD1@注解">5600 时，N=5

以上就是SOLIDWORKS函数相关的解析和用法，如有补充欢迎留言交流。有需要进一步了解SOLIDWORKS可以 点击了解