从悬臂梁了解SOLIDWORKS Simulation中有限单元法的应用

生活里的 “悬臂梁”，竟藏着有限元的奥秘！你家的阳台、起重机的吊臂、网红建筑的悬挑平台…… 这些 “一头固定、一头悬空” 的悬臂梁，看似简单却暗藏力学玄机。

工程师如何确保阳台不晃、吊臂承重达标？答案藏在 SOLIDWORKS Simulation 的有限单元法（FEM）里！今天就以悬臂梁为载体，手把手教你看懂有限元分析的核心逻辑～

先搞懂：有限单元法到底是什么？

简单说，有限单元法是把复杂结构 “拆碎了算” 的智慧：

1.离散化：将悬臂梁分成无数个小单元（比如三角形、四边形网格），就像切蛋糕一样切块分析；

2.单元求解：给每个小单元套用力学公式，计算应力、应变；

3.整体合成：把所有单元的结果整合，还原整个结构的力学响应。

核心优势：再复杂的结构（比如变截面、异形悬臂梁），都能精准算出受力情况，比纯理论计算更高效！

三种方法解决悬臂梁问题

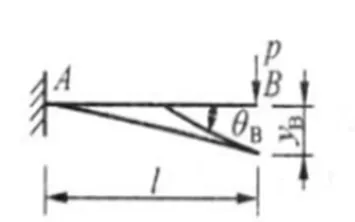
我们在SOLIDWORKS中通过结构件生成一个截面为10*10mm长度为150mm的梁。假设将其左端固定，对其右端施加一个150N的集中力。接下来我们通过三种方法解决悬臂梁的受力问题。

1.经典力学

我们已知简单载荷单独作用下梁的变形，其最大挠度计算公式为1.1所示

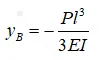
(1.1)

其端截面转角计算公式为1.2所示

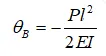
(1.2)

其中P为载荷，l为悬臂梁长度、E为弹性模量此次取210000MPa，I为惯性二次矩，可以通过SOLIDWORKS截面属性得到为833.33mm4。

我们将上述数据代入式1.1与1.2中，可以得到次工况下的悬臂梁最大变形约为-0.6429mm，最大转角为-6.429e-3rad。依据经典力学，我们还可以求其应力、反力等相关参数，本文仅以转角与位移作为最终结果，其余感兴趣的读者可以自行计算。

2、Simulation 计算

通过SOLIDWORKS Simulation计算悬臂梁受力，选用梁单元并设定网格控制为10个。因为此算例比较简单，边界条件的设置不再赘述。最后我们可得其最大位移为-0.6451mm，最大转角为-6.429e-3rad

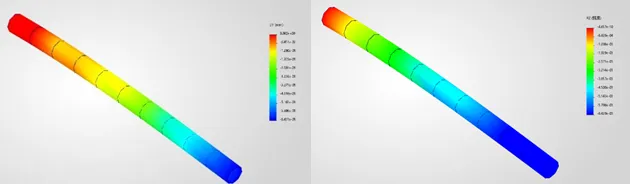
3、有限单元法

大家可能会很好奇，Simulation这一类的仿真软件是如何得出计算结果的，我们第三个有限单元法就是第二个方法的书面表达。

首先，对于Euler-Bernoulli 梁单元的伸缩及弯曲综合的刚度矩阵公式已知为式1.3，具体推导读者可自行查找相关资料。

(1.3)

首先对悬臂梁进行离散化，本例中，我们仅假设共1个单元，2个节点。故可以得到节点位移列阵为

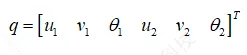
(1.4)

节点外载列阵为

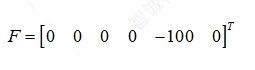
(1.5)

节点支反力列阵为

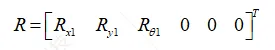
(1.6)

综合得到节点载荷列阵为

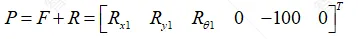
(1.7)

因为一共只有一个单元，故其局部坐标系与全局坐标系一致不需要进行转换，我们可以直接得到总体的刚度矩阵为

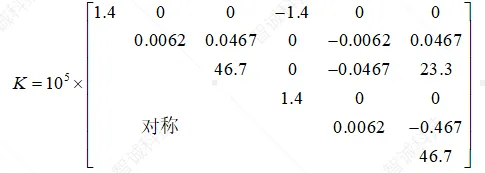
(1.8)

综上我们就可以得到一个总的刚度方程

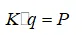
(1.9)

该问题的边界条件是u1=v1=θ1=0，另本次仅计算位移与转角对于反力的计算读者可以自行计算，故处理该边界条件后的刚度方程为

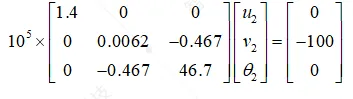
(1.10)

解得

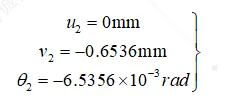
(1.11)

最后我们综合对比上述三种方法的结果，以经典力学为基准SOLIDWORKS Simulation与有限单元法的结果误差极小。对于有限单元法而言，由于本例仅列举1单元2节点，效率不比在有限元软件中进行计算。若碰到形状复杂的连续体或非结构件，难以通过手动计算这些高阶的偏微分方程，故有限元软件大大提高了有限单元法的计算效率。

当前市面上的有限元软件，面对连续体的结构强度问题基本都以有限单元法作为计算方法，许多读者可能会对有限元软件的精度问题产生怀疑，但归根结底商用有限元软件只是通过计算机去进行我们本次方法三的计算过程，并无不同。其中SOLIDWORKS Simulation通过其设计仿真一体化的概念，将仿真验证与设计并行，大大加快了产品设计、更新的进程。